Regularized stochastic algorithms with application to deep neural networks
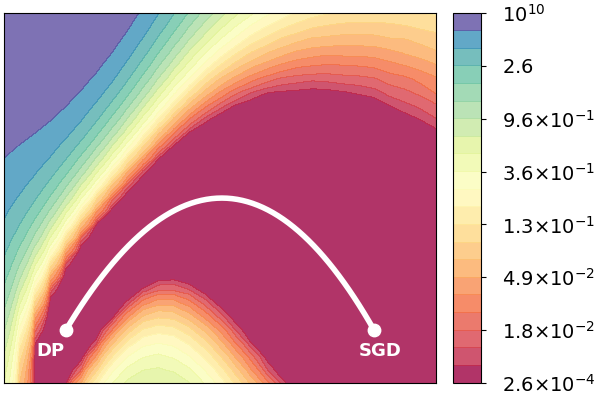
My goal is to develop a family of provable stochastic algorithms with regularization, that is generically applicable to many machine learning problems, such as regression, principal component analysis and deep learning. A variant of our algorithm with $\ell_1$ penalty, called directional pruning (DP), finds a solution in the same minimum valley where SGD is located on the deep learning loss landscape of CIFAR100, but with over 90% sparsity (left panel in the figure below). For large scale dataset like ImageNet, DP is competitive in the high sparsity regime relative to other methods, as shown in the right panel below where our performance is marked by red crosses.

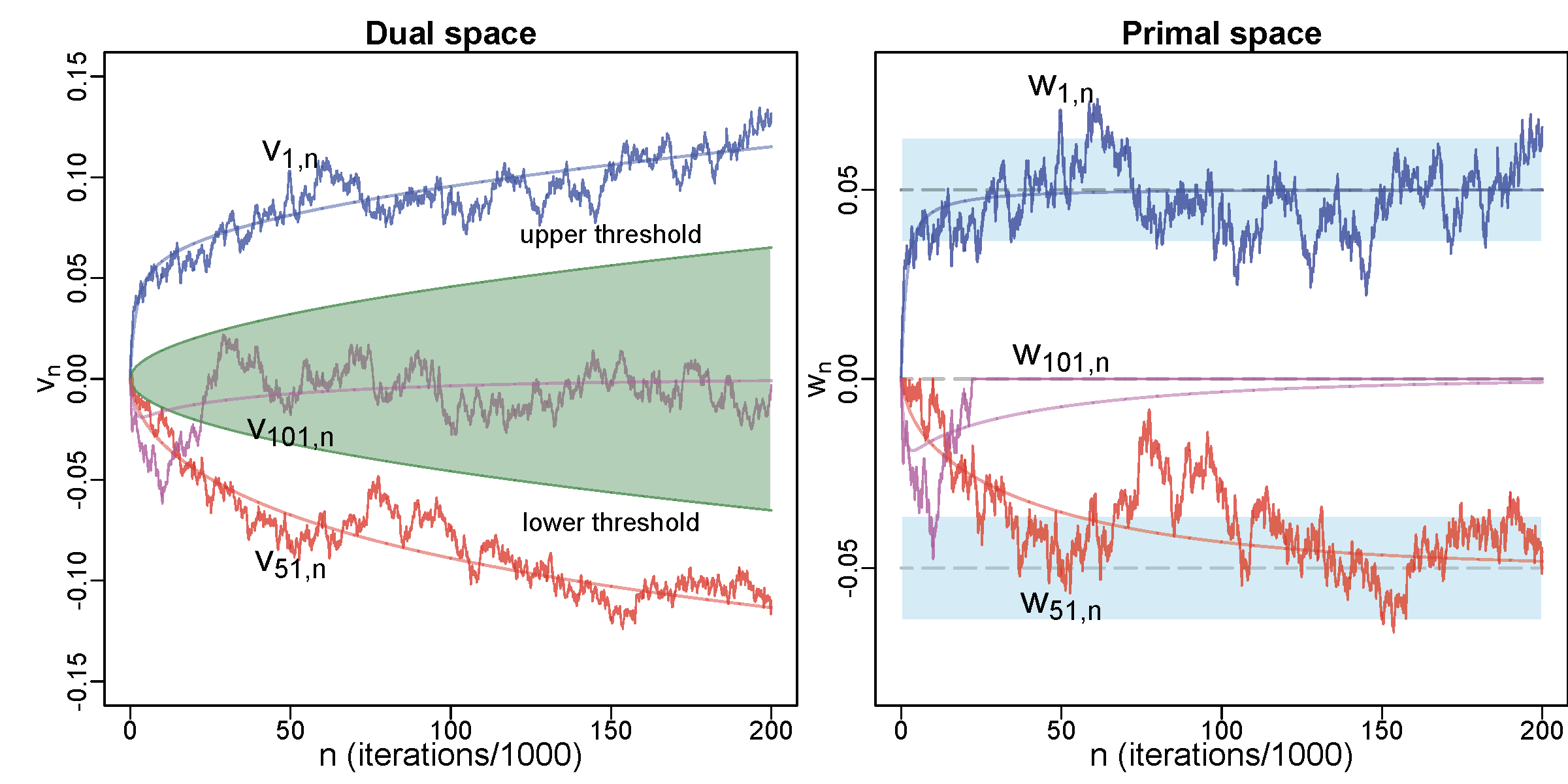
The provability of our algorithm is obtained by two steps. The first is the observation that our algorithm has a mirror desent behavior as it updates a stochastic process in the dual space, and then a mirror map takes the process to the primal space. Next, after recognizing that the process in the dual space is a Markov process, we approximate it with a stochastic differential equation rigorously in the sense of weak approximation. The figure below shows the behavior of three coordinates of our algorithm with $\ell_1$ regularization. In this case the mirror map is a soft-thresholding operator corresponding to the green shaded area in the dual space. Since $v_{101}$ lies mainly in the green area, it is thresholded to 0 in the primal space. Our theory approximates the zigzaging empirical trajectories by smooth curves, which is the solution of an multivariate ordinary differential equation, and captures their random variation in the primal space by the confidence bands in blue.
Our theory can be used to study intriguing interactions between regularization and a complex loss landscape in optimization problem like deep learning, and to obtain theoretical guarantees such generalization bound. Our method has been applied by AutoFIS and structural directional pruning.