Nonparametric quantile regression in social science
Quantile regression is useful for exploring a specific conditional quantile or even the entire conditional distribution of a response variable. Lower quantiles usually correspond to risk, for example the value at risk that financial institutions are required to report at a regular basis. Nonparametric modeling enhances the quantile regression by alleviating the trouble of specifying a regression function, at the cost of a more subtle model tuning.
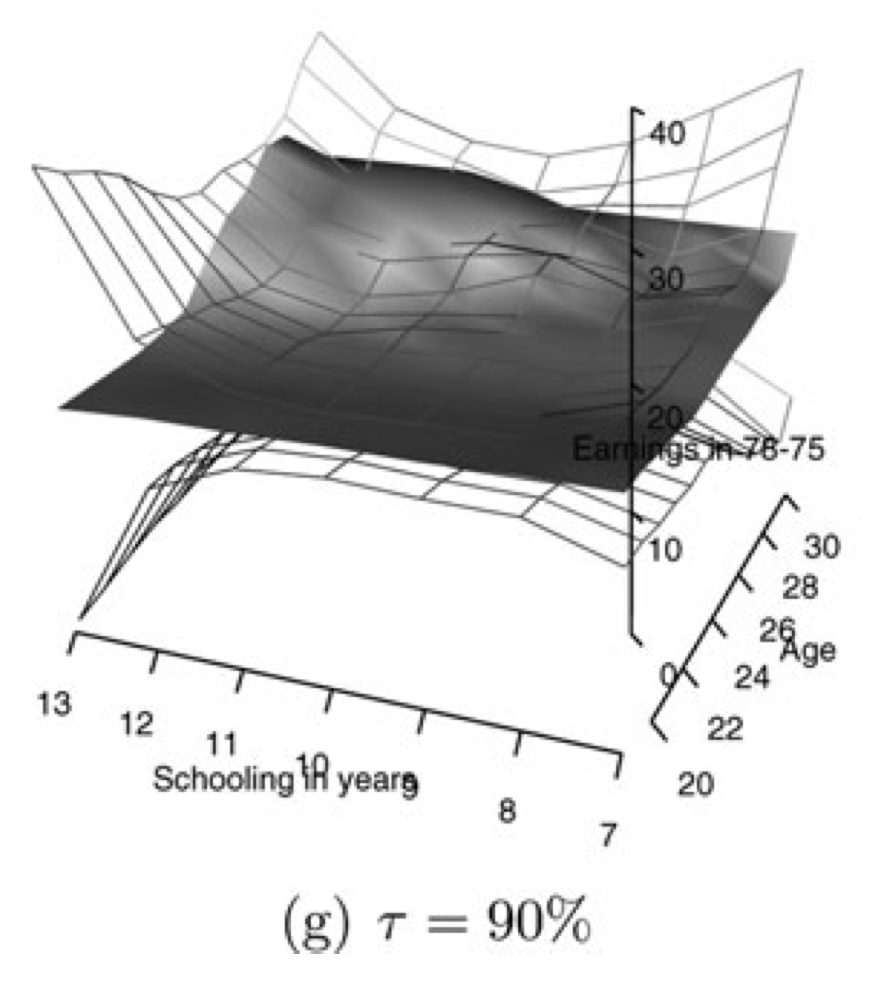
My goal is to develop nonparametric quantile regression and statistical inference tools to study data from social science. For example, in Chao et al. (2021), I estimated lower tail quantile factors from the daily stock returns 230 financial institutions around the globe. Using the factor as a proxy of systemic risk, quantifying which insititution has a higher systemic risk association is possible by checking its score on the factor, and this score (the color in the left panel) is nicely correlated with their laverage and market value. In Chao et al. (2017), I estimated the quantile treatment effect of the National Supported Work program on the income conditional on the schooling years and age. I developed a novel nonparametric quantile regression bootstrap, and used it to show that the treatment effect on income varies with the quantile levels, which is unable to be discovered by usual regression methods.
My vision is to apply quantile regression to broader domains of social science. For example, to educational science to study the different features associated with low performing and high performing students.